Point-Biserial, Phi Coefficient, Biserial, and Tetrachoric Correlation: 4 Important Types of Correlation

Introduction

In psychological and educational research, not all variables are continuous. Many important variables — such as gender, pass/fail outcomes, yes/no responses, or item correctness — are dichotomous (i.e., having only two categories). While Pearson’s and Spearman’s correlation coefficients are widely used for continuous and ordinal data, specialized correlation measures are necessary when dealing with dichotomous or categorical variables.

Correlation

Read More- Experimental Design

Understanding Dichotomous Data

Before delving into these correlations, it’s essential to distinguish between two types of dichotomous variables:

• • True (Natural) Dichotomy: A variable that inherently has only two categories (e.g., male/female, yes/no).
  • Artificial (Dichotomized) Dichotomy: A continuous variable that has been artificially split into two categories (e.g., income categorized as “low” or “high”).

This distinction guides the choice between point-biserial, biserial, phi, and tetrachoric correlations.

1. Point-Biserial Correlation

The point-biserial correlation is used when one variable is continuous and the other is a true dichotomy. For example- Investigating the correlation between gender (male/female) and math test scores.

Formula

Assumptions

• • The continuous variable is normally distributed within each group
  • The dichotomous variable is a true dichotomy

Interpretation

• • Like Pearson’s r, values range from -1 to +1
  • Indicates strength and direction of the relationship

2. Phi Coefficient

The phi coefficient measures the correlation between two naturally dichotomous variables. For example- Analyzing the association between gender (male/female) and voting behavior (voted/did not vote).

Formula

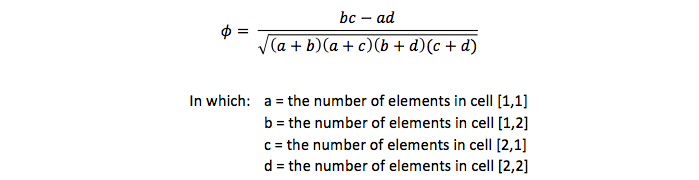
Phi-Coefficient Correlation

Assumptions

• • Both variables are naturally dichotomous
  • Frequencies are not too small (expected counts > 5 generally)

Interpretation

• • Similar to Pearson’s r: ranges from -1 to +1
  • A ϕ of 0 = no association; +1 or -1 = perfect association

3. Biserial Correlation

The biserial correlation is used when one variable is continuous and the other is an artificial dichotomy i.e., a continuous variable that has been dichotomized for analysis. For example- Correlating IQ scores (continuous) with whether a student is “high ability” or “low ability” (based on a cut-off score).

Formula

Assumptions

• • The underlying dichotomous variable is actually continuous in nature
  • Data follow a normal distribution
  • The dichotomization is arbitrary or artificial

Interpretation

• • Like Pearson’s r, ranges from -1 to +1
  • Stronger correction than point-biserial in certain conditions
  • May overestimate the strength of relationship if assumptions are violated

4. Tetrachoric Correlation

Tetrachoric correlation estimates the correlation between two continuous variables that have both been artificially dichotomized. For example- Assessing the latent relationship between attitude toward school and academic motivation, when both have been categorized into high/low based on arbitrary thresholds.

Assumptions

• • Both dichotomous variables are artificial or derived from continuous distributions
  • Underlying distributions are normal
  • Cells in 2×2 table are not too small

Computation

The formula for tetrachoric correlation is complex and not easily computed by hand. It is typically estimated using iterative or maximum likelihood methods, which are available in statistical software like R, SPSS, and Stata.

Interpretation

• • Approximates the Pearson correlation between the underlying continuous variables
  • Best used when both variables are conceptually continuous but categorized for convenience or due to design limitations

Conclusion

Understanding specialized correlation coefficients—point-biserial, phi, biserial, and tetrachoric—is essential for accurately analyzing relationships involving categorical or dichotomous data. Each method has specific assumptions, formulas, and applications that make it uniquely suitable for different research contexts in psychology and education.

By applying the appropriate correlation type, researchers can more precisely detect, describe, and interpret associations in their data, ultimately improving the validity and impact of their findings.

References

Guilford, J. P., & Fruchter, B. (1978). Fundamental Statistics in Psychology and Education. McGraw-Hill.

McCall, R. B. (2001). Fundamental Statistics for Behavioral Sciences. Wadsworth.

Howell, D. C. (2012). Statistical Methods for Psychology (8th ed.). Cengage Learning.

Crocker, L., & Algina, J. (2008). Introduction to Classical and Modern Test Theory. Cengage Learning.