3 Important Types of Factorial Designs

Introduction

Research in psychology and behavioral sciences often involves investigating the effects of multiple variables simultaneously. Factorial designs provide a robust framework for conducting such research by enabling the analysis of not just the isolated effects of individual variables, but also their interactions.

Read More- Reliability in Testing

1. Simple Factorial Designs

A simple factorial design involves the simultaneous manipulation of two or more independent variables (factors), each having two or more levels. The key feature is the full crossing of factors: every level of one independent variable is combined with every level of the other. This produces multiple experimental conditions (cells), each representing a unique combination of factor levels.

For example, a 2 × 3 factorial design means:

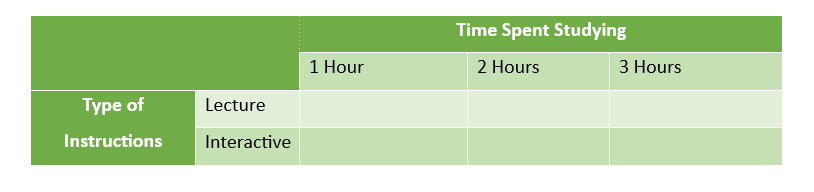
2*3 Factorial Design

• • Factor A has 2 levels (e.g., type of instruction: lecture vs. interactive),
  • Factor B has 3 levels (e.g., time spent studying: 1 hour, 2 hours, 3 hours),

resulting in 6 unique combinations.

The design allows researchers to test:

• • Main effects: The separate impact of each independent variable on the dependent variable.
  • Interaction effects: Whether the effect of one independent variable depends on the level of the other.

Example

Imagine a cognitive psychologist interested in how study techniques and sleep duration affect memory retention. They design an experiment with:

• • Factor A: Study technique (2 levels): Repetition vs. elaborative rehearsal.
  • Factor B: Sleep duration (3 levels): 4 hours, 6 hours, 8 hours.

Participants are randomly assigned to one of the six conditions (e.g., elaborative rehearsal + 6 hours sleep). Memory retention is measured through recall tests. The researcher analyzes:

• • Main effect of study technique: Does elaborative rehearsal outperform simple repetition overall?
  • Main effect of sleep: Does sleep duration impact memory regardless of technique?
  • Interaction effect: Does the benefit of elaborative rehearsal increase with longer sleep?

Advantages

Some advantages include-

• • Efficiency: More data points from one experiment than from multiple single-variable studies.
  • Interaction insights: Reveals how variables combine in real-life scenarios (e.g., studying and sleep).
  • Comprehensive analysis: Tests multiple hypotheses simultaneously.

Limitations

Here are some limitations-

• • Complexity: More factors mean more combinations, complicating design and analysis.
  • Sample size requirements: More cells require larger samples to ensure statistical power.
  • Interpretation challenges: Interactions can be complex and counterintuitive.

2. Factorial Designs with Covariates 

A factorial design with covariates incorporates a statistical control mechanism called Analysis of Covariance (ANCOVA). Here, covariates—continuous variables not manipulated in the study—are measured and statistically adjusted to reduce error variance in the dependent variable. This makes it easier to detect the effects of the independent variables (factors).

Covariate

Covariates typically represent variables that may influence the dependent measure but are not of direct interest (e.g., pre-existing ability, age, baseline performance).

In ANCOVA-enhanced designs:

• • Researchers collect data on covariates before administering treatments.
  • Statistical analyses adjust group means by “controlling” for these covariates.
  • The adjusted means reflect the effects of the experimental factors net of covariate influence.

Example

Consider an education researcher evaluating how teaching methods and classroom settings affect student achievement. The design:

• • Factor A: Teaching method (2 levels): Traditional lecture vs. collaborative learning.
  • Factor B: Classroom setting (2 levels): Standard vs. technology-enhanced.
  • Covariate: Students’ prior knowledge (measured by a pre-test score).

Students are randomly assigned to one of the four conditions (e.g., collaborative learning + technology-enhanced). The researcher uses ANCOVA to adjust post-test scores based on pre-test performance. This removes the confounding effect of varying prior knowledge levels, isolating the effects of teaching method and classroom setting.

Advantages

Some advantages include-

• • Increased precision: Adjusts for pre-existing differences, reducing error variance.
  • Smaller sample size: More precise estimates allow detection of effects with fewer participants.
  • Control of nuisance variables: Provides cleaner insights into the main factors of interest.

Limitations

Here are some limitations-

• • Assumptions: Covariates must relate linearly to the dependent variable, and the relationship should be consistent across groups (homogeneity of regression slopes).
  • Measurement accuracy: Covariates must be measured reliably; error in covariates can bias results.
  • Interpretation complexity: Adjusted means can be less intuitive for readers.

3. Randomized Block Factorial Designs

A randomized block factorial design introduces a blocking variable, which represents a known source of variability (e.g., gender, age, baseline skill). Participants are grouped (blocked) based on this variable, and within each block, they are randomly assigned to all combinations of experimental conditions.

Blocking in Factorial Design

This design improves sensitivity by:

• • Reducing within-group error variance caused by the blocking variable.
  • Allowing for analysis of both block effects and interaction effects between blocks and treatment factors.

Example

Imagine a health researcher studying how exercise type and diet affect weight loss, controlling for gender as a blocking factor:

• • Factor A: Exercise type (2 levels): Cardio vs. strength training.
  • Factor B: Diet (2 levels): Low-carb vs. low-fat.
  • Blocking variable: Gender (male, female).

Within each gender block, participants are randomly assigned to one of the four combinations (e.g., male + strength training + low-fat diet). This ensures gender differences are balanced across conditions. Analysis considers:

• • Main effects: Do exercise type and diet affect weight loss?
  • Block effects: Are there gender differences in weight loss?
  • Interaction effects: Does the effect of exercise and diet differ by gender?

Advantages

Some advantages include-

• • Enhanced precision: Reduces variability caused by known confounders.
  • Efficient use of participants: Essential when participant availability is limited.
  • Improved power: Easier detection of significant effects.

Limitations

Here are some limitations-

• • Design complexity: Requires careful planning of blocks and random assignments.
  • Assumptions: Assumes consistency of blocking effects across conditions.
  • Logistical challenges: Managing blocked assignments can be operationally demanding.

Conclusion

Factorial designs—simple, covariate-adjusted, and blocked—form the backbone of rigorous experimental research in psychology and behavioral sciences. Each design enables researchers to dissect complex interactions, control for confounders, and enhance statistical power. The choice of design depends on research objectives, resource constraints, and the nature of the variables involved.

• • A simple factorial design is best when exploring interactions among independent variables.
  • A factorial design with covariates (ANCOVA) is ideal for controlling measured confounding variables.
  • A randomized block factorial design excels when participant characteristics need balancing to reduce variability.

By thoughtfully selecting and implementing the appropriate factorial design, researchers can uncover nuanced insights into the interplay of variables shaping human behavior.

References

Shaughnessy, J. J., Zechmeister, E. B., & Zechmeister, J. S. (2014). Research Methods in Psychology (9th ed.). McGraw-Hill Education.

Singh, A. K. (2014). Tests, Measurements and Research Methods in Behavioural Sciences. Bharati Bhawan Publishers.